Science thrives on an open exchange of arguments and a plurality of perspectives. Scientific discussions should be open, frank and blind: only arguments should matter, not who presents them. Different viewpoints strengthen the scientific debate, and the inclusion of women and minorities in science will only contribute to this. Understanding the role of gender in science is crucial for improving the representation of women.

A recent paper about the role of gender in mentorship finds that protégés with female mentors show a lower citation impact than protégés with male mentors. This paper, which we refer to as the mentorship paper in this blog post, has been received quite critically. There have even been calls to retract the paper, which in turn have been criticised as well, both on Twitter and elsewhere. Critics of the paper have raised a number of concerns, for example about the data and the operationalisation of the idea of mentorship. In this blog post, we discuss a different aspect of the paper, namely the challenge of identifying causal effects of gender. This is a major challenge not only for this specific paper, but also for many other studies on the role of gender in science.

Inequality, disparity and bias

Although many papers use the term “gender bias”, its meaning is not always clear. Instead of “gender bias”, some studies use the term “gender disparity”, while others employ “gender inequality”, “gender difference” or occasionally "gender gap". The different terms sometimes seem to be used interchangeably, making it unclear what researchers try to communicate with each term. To facilitate a clear discussion, we propose a more precise terminology. Such an improved terminology may contribute to a better understanding of the policy implications of a study. This is also relevant in the context of the above-mentioned mentorship paper.

We propose to define a “gender inequality” or a “gender difference” simply as any observed difference between people with a different gender.

Our proposal is to use the term “gender disparity” to refer to any difference between people with a different gender that is causally affected by their gender. This means that if a woman had been a man (or vice-versa), the outcome of interest would have been different.

The strongest term is “gender bias”, which we propose to define as any difference between people with a different gender that is directly causally affected by their gender. Similar to a gender disparity, this means that if a woman had been a man, the outcome of interest would have been different. However, whereas a gender disparity may be the result of an indirect causal pathway from someone’s gender to a particular outcome, a gender bias is a direct causal effect.

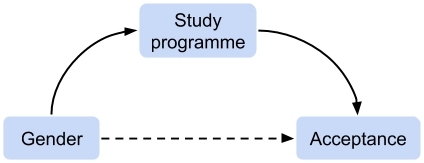
To clarify the distinction between a gender disparity and a gender bias, consider the example of being accepted at a prestigious university. Suppose that the acceptance rates for men and women are equal for each study programme, but that some study programmes have lower acceptance rates than others. If women apply more often for study programmes with lower acceptance rates, this results in a lower overall acceptance rate for women. In this case, there is a gender disparity in the overall acceptance rate. However, because the causal effect is mediated by study choice, this gender disparity should not be called a gender bias (see Figure 1). You may recognise this as an example of the famous Simpson’s Paradox, which actually took place in Berkeley in 1973. In contrast, suppose that a change in someone’s gender on an application form affects the acceptance decision. In that case, gender does have a direct effect on acceptance, which means there is a gender bias in acceptance rates.

The distinction between gender inequalities, gender disparities and gender biases is important in discussions about interventions that aim to improve participation of women in science. In the case of a gender disparity or gender bias, there is a causal effect of gender on a particular outcome. This provides a clear rationale for considering to intervene somewhere in the system. The distinction between gender disparities and gender biases helps to determine where in the system an intervention seems more appropriate. To illustrate this, let us revisit the above example of being accepted at a prestigious university. If the effect of gender on acceptance rates is mediated by study choice, there is a gender bias in the choice of study programme, not in acceptance rates. Therefore, an intervention targeted at study choice (e.g., making certain study programmes more attractive for women) seems more reasonable than an intervention targeted directly at acceptance rates (e.g., imposing a minimum acceptance rate for women). Whether an intervention is desirable can still be debated, but the distinction between gender disparities and gender biases helps to clarify where in the system an intervention might best be considered.

All gender disparities are also gender inequalities, but the opposite does not hold: not all gender inequalities are gender disparities. This complicates matters greatly in many studies, including the above-mentioned mentorship paper. The reason is a problem known as collider fallacy.

Collider fallacy

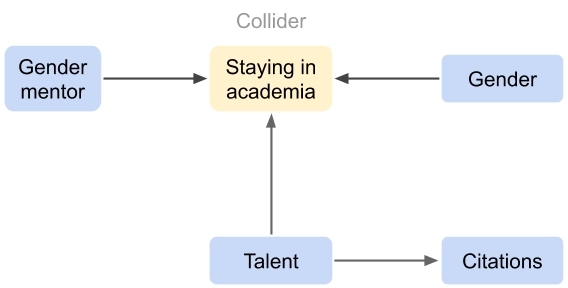
To illustrate the problem of collider fallacy, we consider a simple causal model describing mechanisms relevant to interpreting the above-mentioned mentorship paper (see Figure 2). In our model, someone’s research talent affects both the citations they receive and the likelihood of staying in academia. Independently of this, someone’s gender and the gender of their mentor also affects the likelihood of staying in academia. More specifically, we assume that having a female rather than a male mentor makes it more likely for a female protégé to stay in academia. In this causal model, there are multiple factors that affect the factor “staying in academia”, making it a collider for those factors.

If we condition on the factor “staying in academia”, for example by controlling for it in a regression model, we introduce a correlation between the gender of the mentor and the research talent of the protégé. In our causal model, female protégés with male mentors are less likely to stay in academia, which means that those who do stay in academia can be expected to be more talented, on average, than their colleagues with female mentors. As a result, having female mentors is correlated with a lower research talent of protégés who stay in academia. Their lower research talent then in turn leads to fewer citations for those protégés. Importantly, however, this correlation does not reflect a causal effect. Instead, it is the result of conditioning on a collider. This example illustrates the problem of conditioning on colliders when studying causal effects. It leads to wrong conclusions.

The problem, unfortunately, is even more daunting. When we collect data, we often use a variable to select the data to be collected. This effectively means that we control for this variable. If the variable acts as a collider, this leads to a collider fallacy. In the mentorship paper, the authors make a selection of the protégés included in the data collection: “we consider protégés who remain scientifically active after the completion of their mentorship period” (p. 2). In our causal model introduced above (see Figure 2), this selection of protégés results in a collider fallacy, leading to the observation that protégés with female mentors receive fewer citations. Depending on the extent to which our causal model captures the relevant causal mechanisms, the main result of the paper may be due to this collider fallacy.

From observations to recommendations

The possibility of a collider fallacy calls into question the policy recommendations made in the mentorship paper. The authors suggest that women should be paired with a male mentor because this has a positive effect on their citation impact. If the above causal model holds true, this suggestion is not correct. In this model, pairing a female protégé with a male mentor reduces the likelihood that the protégé stays in academia, which means that those protégés who do persevere in academia are likely to be more talented and to receive more citations. In our terminology: the difference between male and female mentors in the citations received by their protégés may be only a gender inequality, not a gender disparity and certainly not a gender bias. Without additional evidence or assumptions, the observed gender inequality does not support the policy recommendations made in the mentorship paper. In fact, given our conjectured causal model, it can be argued that one should do the opposite of what is suggested in the paper: to increase female participation in science, female protégés should be paired with female mentors.

Although many eyes are now on the mentorship paper, the state of affairs in many other papers on gender differences in science is not necessarily better. In an excellent and comprehensive review of the literature on gender differences in science funding, the lack of causal knowledge was identified as a sore point. The literature regularly discusses gender inequalities, disparities and biases without having a clear causal framework, possibly leading to ill-conceived policy recommendations, which in some cases may actually hurt progress towards a better gender balance. We hope that our proposed definitions of gender inequality, gender disparity and gender bias contribute to an improved appreciation of the causal intricacies in studying the role of gender in science.

As already mentioned, some calls have been made to retract the mentorship paper. We do not support such calls. The policy recommendations made in the paper may be incorrect and may even be harmful to the representation of women in science. However, discussions about the correct interpretation of analyses like the one reported in the mentorship paper are highly complex and usually do not lead to a clear-cut answer. Papers should be retracted in the case of factual mistakes or scientific misbehaviour. Retracting a paper because of disagreements about the interpretation of the findings would be deeply problematic. We should exchange arguments and discuss their merits in an open and honest debate. If we lose this, we are fighting a lost cause.